Java集合—LinkedList

1. 原理

LinkedList 底层是双向链表，对应的是链表这种基本的数据结构。同样，它的大多数特性都来源于链表。

我们看看 LinkedList 类的继承结构：

1
2
3

public class LinkedList<E>
    extends AbstractSequentialList<E>
    implements List<E>, Deque<E>, Cloneable, java.io.Serializable

如代码所示，LinkedList 实现了 Deque、Cloneable、Serializable。

Deque：Deque 是 Queue 的子接口，双向队列
Cloneable：支持克隆
Serializable：支持序列化

缺点：

不支持随机读，读取数据需要遍历。时间复杂度O(n) 。

优点：

非常适合频繁的插入
可以当做队列来使用

2. 源码解析

先看一下比较重要的静态内部类 Node，代码如下:

private static class Node<E> {
    E item;
    Node<E> next;
    Node<E> prev;

    Node(Node<E> prev, E element, Node<E> next) {
        this.item = element;
        this.next = next;
        this.prev = prev;
    }
}

item: 存储每个 Node 的数据
next: 指针指向下一个节点
prev: 指针指向上一个节点

来，画个 LinkedList 的基础结构图。

LinkedList 结构大致如上图所示，前后两个 Node 互相指向对方。头部的 prev 和尾部的 next 指向空。下面所有的操作都是基于这个基础结构图。

2. 1 插入操作

链表的插入操作不需要像数组那样进行移位操作，所以性能还是比较高的。插入操作分为以下三种情况。

2.1.1 头部插入

来，上源码：

1
2
3

public void addFirst(E e) {
    linkFirst(e);
}

private void linkFirst(E e) {
    final Node<E> f = first;
    final Node<E> newNode = new Node<>(null, e, f);
    first = newNode;
    if (f == null)
        last = newNode;
    else
        f.prev = newNode;
    size++;
    modCount++;
}

接下来，我们边看代码边画图。

第 2 行代码，创建一个指针 f ，指向 first 节点，图如下：

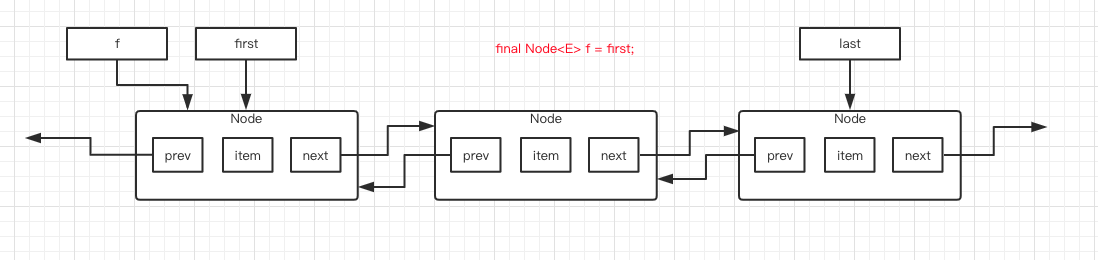
第 3 行代码，新建了一个 Node 对象，名字是 newNode ，prev 指向为 null ，item 元素是 e ，next 指向 f 。而 f 是指向 first 节点的，所以图就变成下面这个样子了。

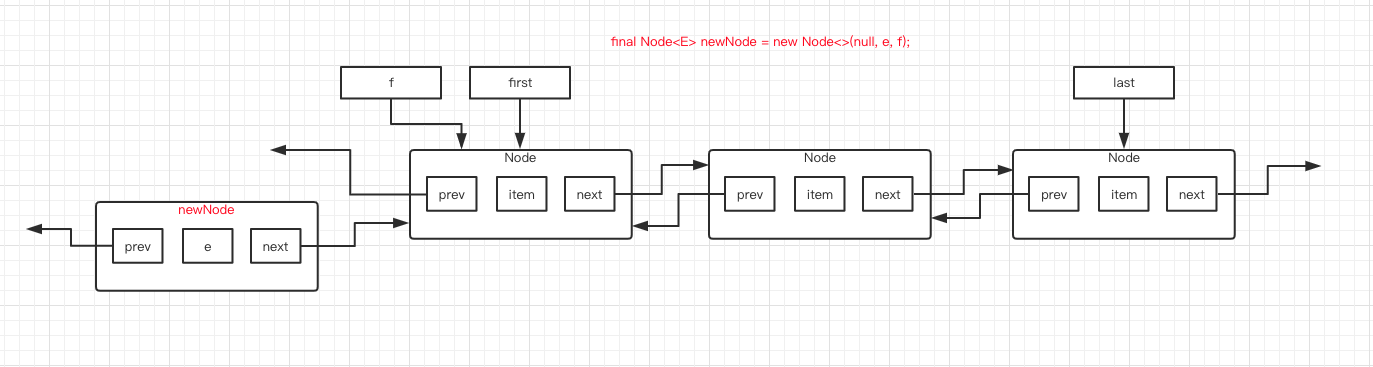
第 4 行代码，将 first 指针指向刚刚创建的 newNode 对象。图如下：

第 5 行代码判断 f 是否为 null ，很明显，f 指向了一个 Node ，不为 null 。于是执行第 8 行代码，将 f 的 prev 指针指向新建的 newNode 。图如下：

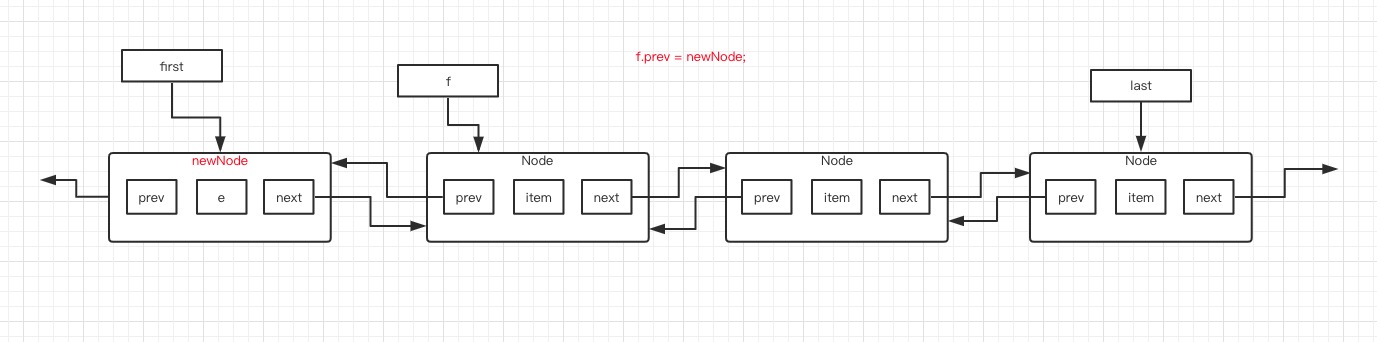
最后执行第 9、10 行代码，size 的值加 1，modCount 的值加 1。

看看最终的图，一个头部插入就结束了。至于多余的这个 f 指针，因为是方法内的局部变量，所以在方法执行完毕之后自动出栈，也就不再指向任何 Node 了。这个 JVM 相关的内容，在此不做过多解释。

2.1.2 尾部插入

addLast(E e) 和 add(E e) 方法都是尾部插入，调用的都是 linkLast 方法。来，上源码：

public boolean add(E e) {
    linkLast(e);
    return true;
}

void linkLast(E e) {
    final Node<E> l = last;
    final Node<E> newNode = new Node<>(l, e, null);
    last = newNode;
    if (l == null)
        first = newNode;
    else
        l.next = newNode;
    size++;
    modCount++;
}

同样，一步一图。

第 2 行代码，新建了一个指针 l 指向 last 节点。如图：

第 3 行代码，新建了一个 Node 对象，名字是 newNode ，prev 指向为 l ，item 元素是 e ，next 指向 null 。而 l 是指向 last 节点的，所以图就变成下面这个样子了。

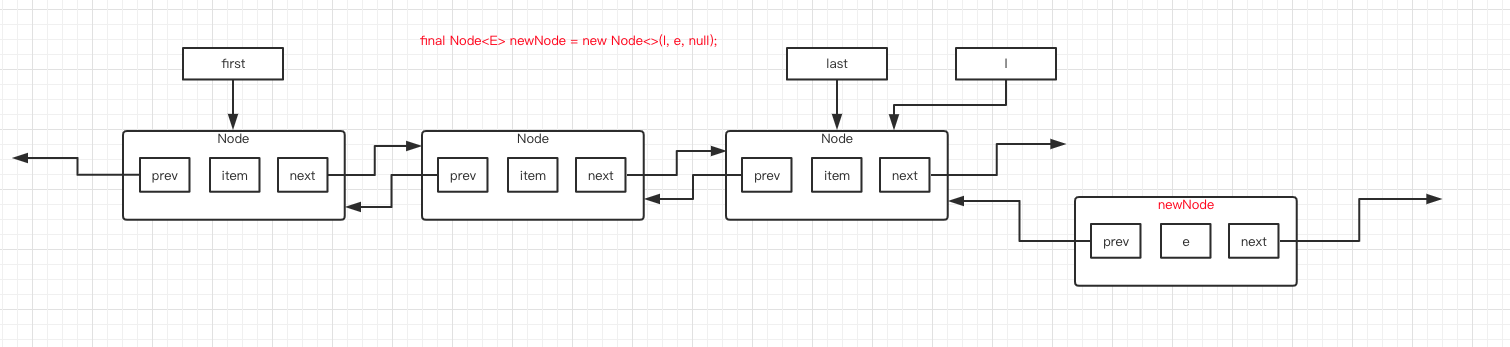
第 4 行代码，将 last 指针指向刚刚创建的 newNode 对象。图如下：

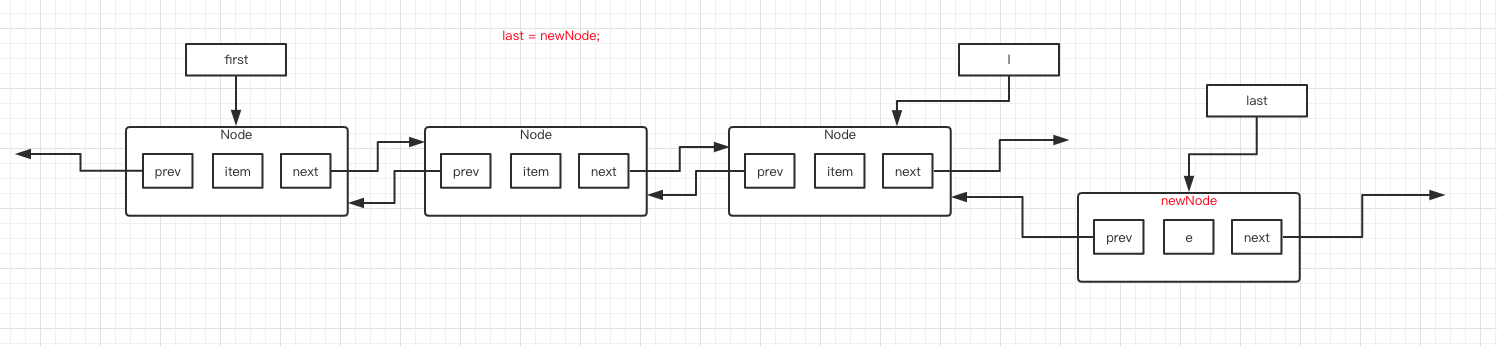
第 5 行代码判断 l 是否为 null ，很明显，l 指向了一个 Node ，不为 null 。于是执行第 8 行代码，将 l 的 next 指针指向新建的 newNode 。图如下：

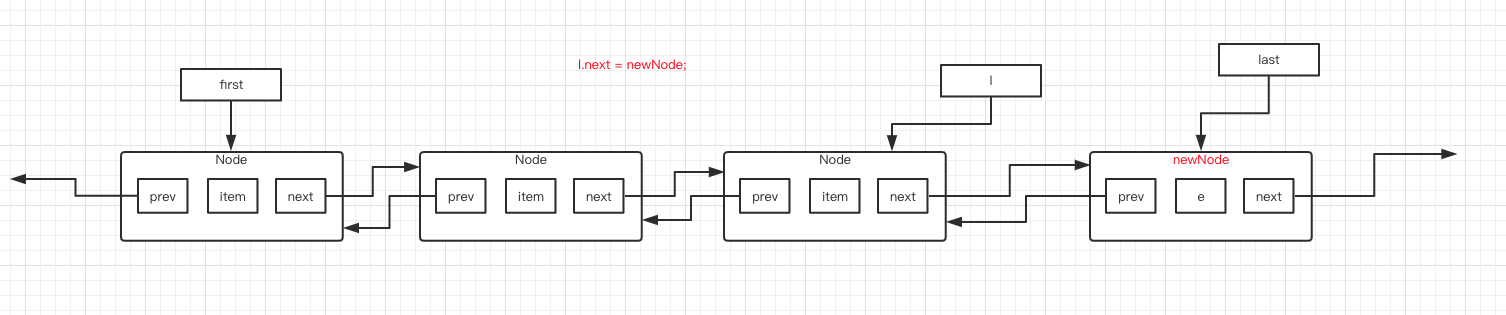
最后执行第 9、10 行代码，size 的值加 1，modCount 的值加 1。和头插法其实很类似。

2.1.3 中间插入

public void add(int index, E element) {
    checkPositionIndex(index);

    if (index == size)
        linkLast(element);
    else
        linkBefore(element, node(index));
}

第 2 行代码是校验 Index 是否越界。

第 4 行代码校验 index 是否等于 size ，如果相等，就是尾插。我们讲的是中间插入，所以直接看第 7 行代码。

node(index) 是获取 index 那个位置对应的 Node ，其实 LinkedList 的 get 方法就是使用的 node(index) 来实现的。底层使用的是二分查找的思想，比较简单，就不分析了。着重看一下 linkBefore 方法。

void linkBefore(E e, Node<E> succ) {
    // assert succ != null;
    final Node<E> pred = succ.prev;
    final Node<E> newNode = new Node<>(pred, e, succ);
    succ.prev = newNode;
    if (pred == null)
        first = newNode;
    else
        pred.next = newNode;
    size++;
    modCount++;
}

同样，我们一步一图，还是基于基础结构图，最开始的图是这样的。

我们假设 Index 为 1 ，此时 node(1) 拿到的就是上图中中间的那个 Node 。

第 3 行代码，此时 succ 就是中间的 Node ，新建一个 pred 指针指向 succ.prev ，而 succ.prev 就是指向的 first 节点。图如下：

第 4 行代码，新建一个 newNode ，它的 prev 指向的是 pred ，next 指向的是 succ ，自身元素是 e ，如下图所示：

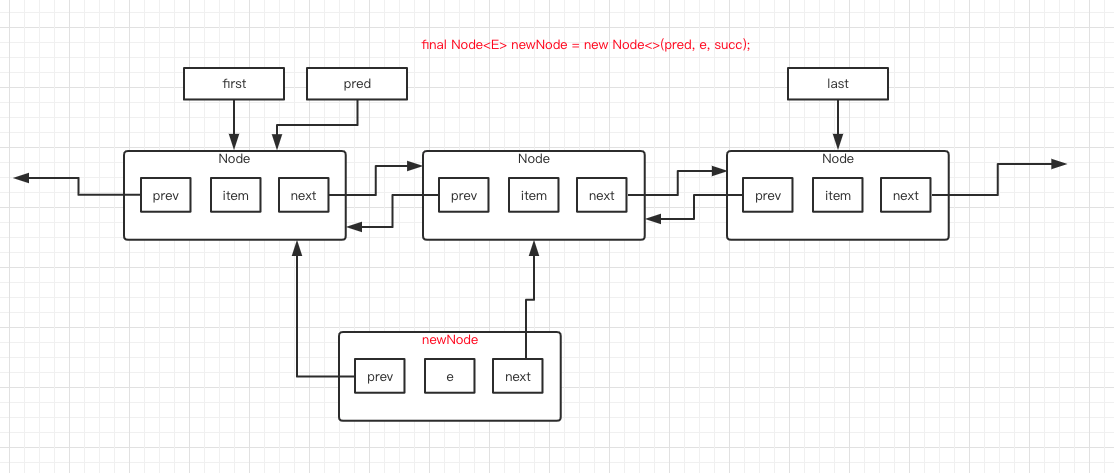
第 5 行代码，将 succ 的 prev 指向 newNode ，如图所示：

第 6 行代码，判断 pred 是否为 null ，很明显不为 null 。执行第 9 行代码，将 pred 的 next 指向 newNode 节点。如图所示：

最后执行第 10、11 行代码，size 的值加 1，modCount 的值加 1 。

2.2. 删除操作

删除操作其实和插入操作比较类似，都是指针的变动。所以这里就只分析中间删除了。头部删除和尾部删除有兴趣的同学自行分析。

2.2.1 中间删除

public E remove(int index) {
    checkElementIndex(index);
    return unlink(node(index));
}

第 2 行校验 index ，直接看 unlink 方法。

E unlink(Node<E> x) {
    // assert x != null;
    final E element = x.item;
    final Node<E> next = x.next;
    final Node<E> prev = x.prev;

    if (prev == null) {
        first = next;
    } else {
        prev.next = next;
        x.prev = null;
    }

    if (next == null) {
        last = prev;
    } else {
        next.prev = prev;
        x.next = null;
    }

    x.item = null;
    size--;
    modCount++;
    return element;
}

同样，我们一步一图，还是基于基础结构图。假设 index 为 1 。node(1) 拿到的就是基础结构图中中间的那个 Node 。此时 x 就是中间那个 Node 。

首先执行 3、4、5 行代码，新建一个 element ，指向 x 的自身元素 item ；新建一个 next ，指向 x 的 next ；新建一个 prev ，指向 x 的 prev 。执行结束后，图如下：

第 7 行代码，判断 prev 是否为 null ，很明显不为 null 。这里如果为 null 的话其实就是头部删除。当然，我们这不是，所以进入第 10、11 行代码。

第 10 行代码，是将 prev 的 next 指向 next 指针，第 11 行代码是将 x 的 prev 指向 null 。执行后如下图所示，红色线条为变动部分。

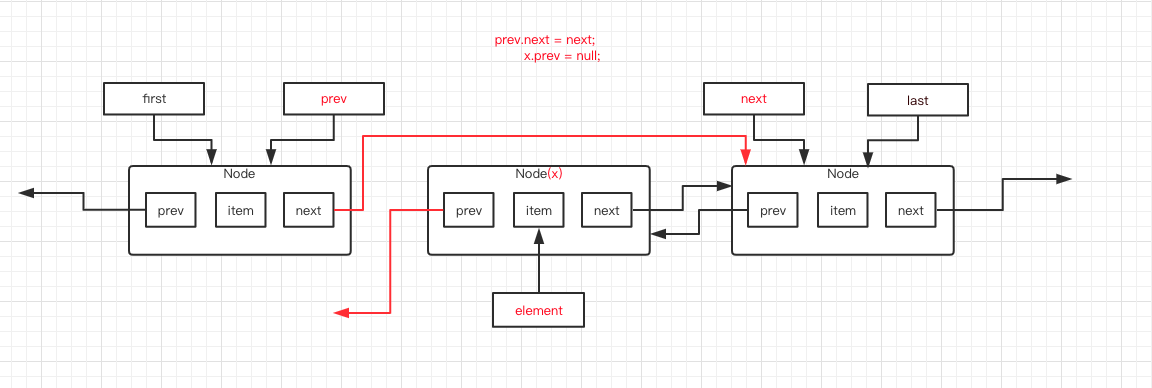
第 14 行代码，判断 next 是否为null ，很明显不为 null 。这里如果为 null 的话其实就是尾部删除。我们这里直接进入第 17、18 行代码。

第 17 行代码，将 next 的 prev指向 prev 指针，第 18 行代码是将 x 的 next 指向 null 。执行后如下图所示，绿色线条为改动部分。

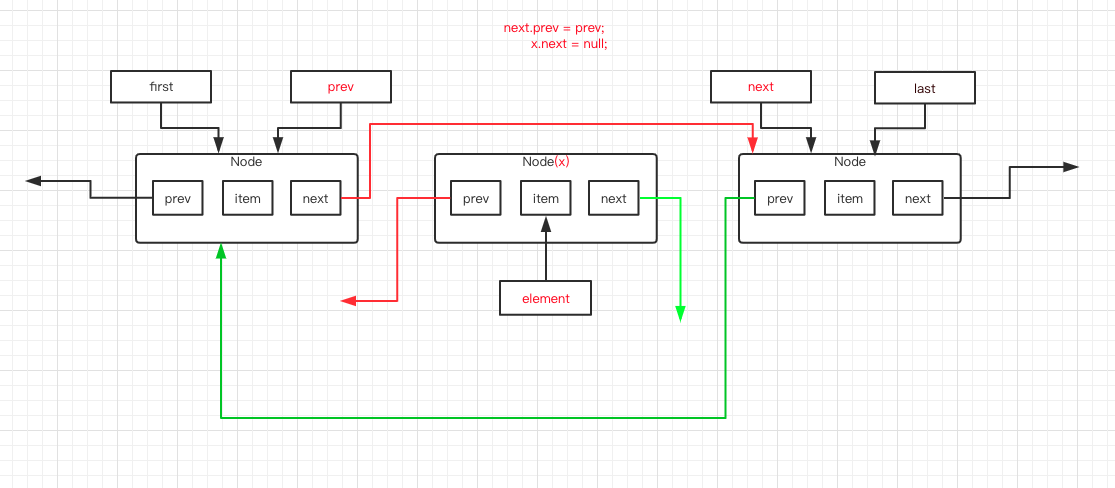
第 21 行代码，将 x 的 item 设置为 null 。此时 x 的 prev 、item、next 都是 null ，便于垃圾回收器进行回收。

第 22、23 行代码太简单，不赘述了。

3. 总结

其实 LinkedList 的底层就是在链表。所以只要搞清楚链表这个基础的数据结构，LinkedList 理解起来也很简单。