Java集合—HashMap之resize方法

2. 源码解析

上一篇文章 Java集合—HashMap之梳理put方法逻辑 已经详细梳理了 put 方法的逻辑，着重讲述了在遇到 hash 冲突时链表是如何一步一步变化的。但是遗留了两个问题，一是扩容方法，二是红黑树结构相关的逻辑。那么这一篇文章，我们就来看看 HashMap 是怎么扩容的。

2.4 resize

在 putValue 方法当中就有 3 个地方使用到了 resize 方法

• 初始化数组，分配内存时
• 链表转化为树时
• 每次新增元素之后都会进行判断是否需要扩容

下面我们结合这 3 个地方来看看 resize 的源码。首先我们看一下 resize 方法的注释。

/**
 * Initializes or doubles table size.  If null, allocates in
 * accord with initial capacity target held in field threshold.
 * Otherwise, because we are using power-of-two expansion, the
 * elements from each bin must either stay at same index, or move
 * with a power of two offset in the new table.
 *
 * @return the table
 */
final Node<K,V>[] resize() {

翻译一下注释：初始化数组或者数组翻倍。如果是初始化（即数组为空），通过初始化的长度 initial capacity 和 threshold 来指定长度。否则，进行扩容，又因为每次扩容都是 2 倍，所以扩容之后元素要么还停留在原来的位置，要么移动 2 的幂次方。

具体扩容之后的偏移量这篇文章会细讲。

老规矩，先上一张图，辅助我们理解 resize 方法的大致流程。

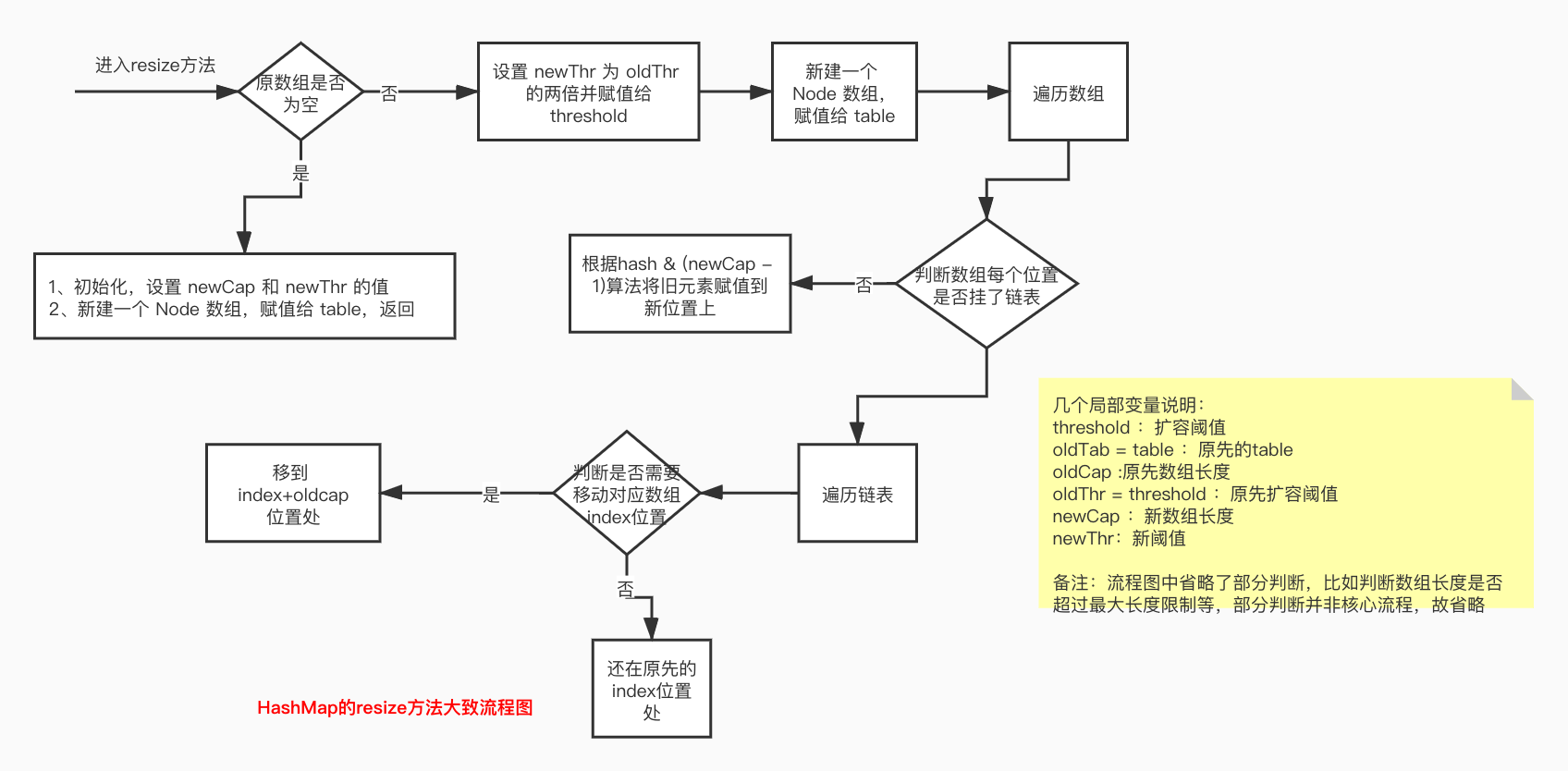
这张流程图只是描述了大致的流程，具体代码实现的细节我们对着源码来看，来，上源码：

final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

源码很长，有的讲源码的博客文章会在代码中写注释，但是我觉得很多东西一两行注释说不清楚。但是我这样写又会导致在看说明的时候还得往上翻看对应的哪一行代码，所以建议大家看的时候开两个窗口，一个看代码，一个看说明。

第 2 ~ 5 行代码是做初始化赋值，没什么好说的。

看第 6 行代码的判断，oldCap > 0 ，很明显，扩容的时候会进这个代码块，第 7 行代码判断是否超过了最大容量，如果是，将阈值 threshold 设置为 int 最大值。否则将 newCap 设置为 oldCap 的两倍，同样 newThr 也是 oldThr 的两倍。

第 15 行代码，是 oldCap 等于 0 并且 oldThr 大于 0 。后面的注释的意思是，如果使用了带有初始化容量的构造函数，此时 oldThr 是大于 0 的。回顾下带有初始化容量的构造函数：

public HashMap(int initialCapacity, float loadFactor) {
    // 省略代码
    this.threshold = tableSizeFor(initialCapacity);
}

如上述代码所示，会将 initialCapacity 经过 tableSizeFor 方法处理之后赋值给 threshold ，此时 oldThr 就会大于 0 。然后进入第 16 行代码，将 oldThr 赋值给 newCap 。那如果我们使用的是无参构造函数呢？很明显，会进入第 17 行代码，给 newCap 和 newThr 设置默认值。

来，小结下：上面的代码总共判断了如下三种情况。之后使用到这三种情况会简称为 1、2、3 。

1. 数组不为空
2. 数组为空，使用带初始容量的构造函数创建的
3. 数组为空，使用无参构造函数创建的

如果 1，会扩容，新数组长度 newCap 为原先两倍；

如果 2，数组长度 newCap 取初始容量（前提是初始容量是合理的，不合理的会自动转化，之前文章提到过）；

如果 3，数组长度 newCap 取默认值；

我们接着往下看第 21 行代码，只有 2 才会 newThr 等于 0 ，第 22 ~ 23 行代码是给 newThr 赋值。

第 26 代码的意思是，无论是新创建初始化的还是扩容的，都将上面代码处理完毕之后得到的 newThr 赋值给 threshold 。

第 28 ~ 29 行新建了一个 Node 数组，然后赋值给 table 。然后进入第 30 行代码，最关键的扩容方法。当然，只有 1 才能进入。我们画一张图，假设 HashMap 目前如下图所示：

第 31 行先对老数组进行遍历，将数组的每个 index 的值赋值给 e，第 33 行代码很容易理解，不为空才继续。图中 index 为 3 的位置为空，就不会进入到 if 分支来。

第 35 行代码是判断 e.next 是否为空，其实就是判断 index 对应位置后面有没有挂链表或者红黑树，图中 index 2 和 4 没有挂链表，会进入第 36 行代码，e.hash & (newCap - 1) 是根据新的数组长度再次进行 hash 算法算出新的 index 方法新数组对应位置上。这个操作被称作 rehash。

比如“张三”扩容前是通过 张三.hash & (16 - 1) 算出的 index 为 2，那么此时 张三.hash & (32 - 1) 可能算出来就是 18 了，如下图所示：

为什么是 18 呢？我们接下来会讲。当然，也有可能 rehash 之后还是在原来的位置 2 上。

第 37 行代码是红黑树的 rehash ，我们后面单独讲。

进入到第 39 行代码，也是这篇文章最重要的链表的 rehash 方法。在分析之前，我们来思考一下，为什么原先在 index 为 2 位置上的元素要么停留在原位，要么跑到 index 为 18 的位置上呢？我们来举个例子：

假设张三的 hash 的后 5 位是 00010（在这种情况下，只有后 5 位比较重要，如果不知道为什么的同学先看看我之前的 hash 优化算法的那篇文章）。

0 0010（张三的hash）

0 1111（n - 1 = 16 -1 = 15）

0 0010

这是在扩容前（初始容量16），张三算出来的 index 是 2 。如果此时扩容，新容量为 32 ，那么 rehash 的结果为

0 0010（张三的hash）

1 1111（n - 1 = 32 -1 = 31）

0 0010

rehash 的结果，index 还是 2，位置不变。

那如果张三的 hash 的后 5 位是 10010 呢？

1 0010（张三的hash）

0 1111（n - 1 = 16 -1 = 15）

0 0010

即 10010 & 15 = 2 ，那此时扩容 rehash 后呢？

1 0010 （张三的hash）

1 1111（n - 1 = 16 -1 = 15）

1 0010

1 0010 的十进制是 18 。我们思考一个问题，18 有什么特殊的含义呢？

18 = 2 + 16 = 2 + oldCap 。我们找到了一个规律，在 rehash 之后，要么停留在原位置，要么移到原 index + 原数组长度的位置上。其实很容易理解，初始化和 （16 - 1）做与运算时，只有低 4 位的 hash 是有意义的，但是扩容的时候，和 （32 -1 ）做与运算时，低 5 位也参与了运算，所以低 5 位的值决定了 rehash 后新的 index 的值。如果低 5 位为 0 ，index 值不变，如果低 5 位为1，则 index 改变，并且在原先基础上加了 2 的 4 次方，即 16 。

依次类推，如果从 32 扩容到 64 ，则低 6 位决定了 index 是否改变，如果改变，在原先基础上加 2 的 5 次方，即 32 。

综上所述：在 resize 方法中，数组 rehash 时，要么停留在原位，要么移到 oldIndex + oldCap 的位置上。

下面我们从第 39 行代码开始分析，我们以数组 index 为 1 的链表为例，首先定义了几个局部变量，然后进行循环，循环退出条件是链表遍历完毕。我们一步步画图分析。此时 j 的值为 1 。

在 33 行代码中，首先是将指针 e 指向 index 为 1 的数组位置，44 代码将 next 指针指向 e.next ，那么图如下所示：

第 45 行代码，e.hash & oldCap ，这个非常非常关键。oldCap 为 16，因为此时 index 为 1，那么 e.hash 的后五位可能为 0 0001，也有可能为 1 0001，和 15 进行与运算之后都为 1 。

0 0001 和 16 进行与运算为 0 ， 1 0001 和 16 进行与运算为 的结果为 16 ，不为 0。所以我们猜测，e.hash & oldCap 等于 0 就是这个位置的元素不需要移位时的处理逻辑，而对应的 52 行代码的 else 就是需要移位的处理逻辑。

那我们就假设“赵小发”和“赵大发”不需要移位，即 (e.hash & oldCap) == 0。

“赵二发”需要移位，即 (e.hash & oldCap) != 0。

进入“赵小发”的循环，此时会进入 45 行代码分支，执行 47 和 50 行代码后，如下图所示：

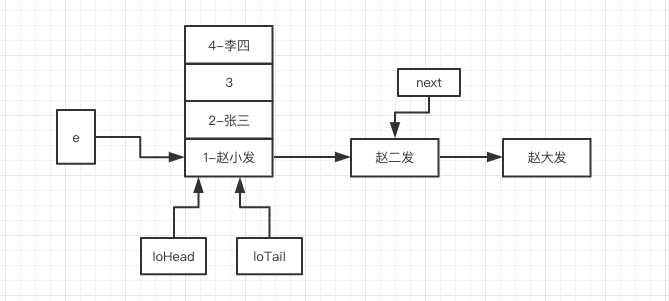
然后千万别忘了，在 59 行 while 循环里面有 e = next，这个时候把 e 指针指向 next ，最终执行完毕之后如下：

进入“赵二发”的循环，首先执行 44 行 next = e.next ，如下图所示：

然后进入到 52 行代码的分支。

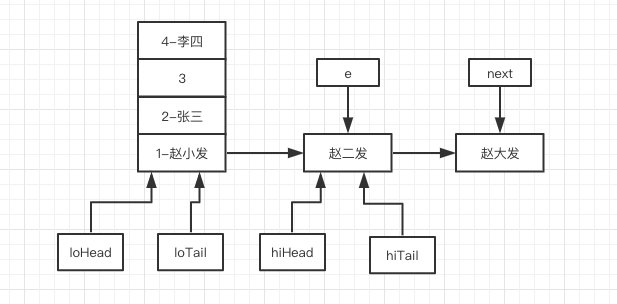
最后依然别忘了 59 的代码 e = next ，最终执行完毕后如下图所示：

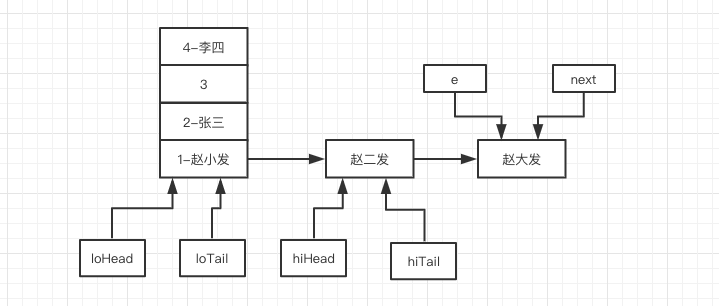
再进入“赵大发”的循环，首先执行 44 行 next = e.next。

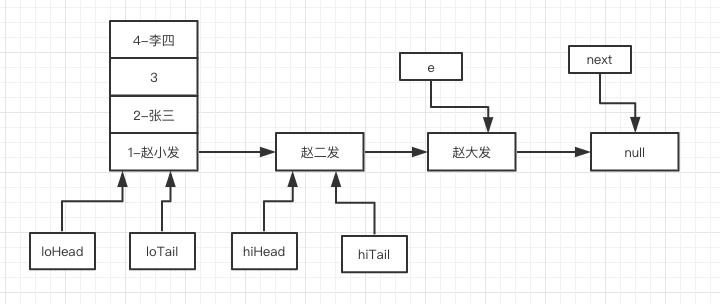
然后会进入 45 行代码分支，但是进入 46 行判断时，此时 loTail 不为空，所以执行第 49 和 50 行代码。

最后依然别忘了 59 的代码 e = next ，最终执行完毕后如下图所示：

最后执行完毕 e 指向 null ，此时退出 while 循环。

最后我们来看 60 ~ 67 行代码。loTail 此时不为 null ，执行 61、62 行，将 loHead 放在新数组的 index 为 1 的位置上。而此时，“赵小发“的数组后面挂着”赵大发“，新数组就会变成下图所示：

然后执行第 64 行代码，此时 hiTail 也不为空，执行 65 行代码，图就会变成下面这样子。

执行第 66 行代码，将 hiHead 放到新数组的 1 + oldCap = 1 + 16 = 17 位置上，如下图所示：

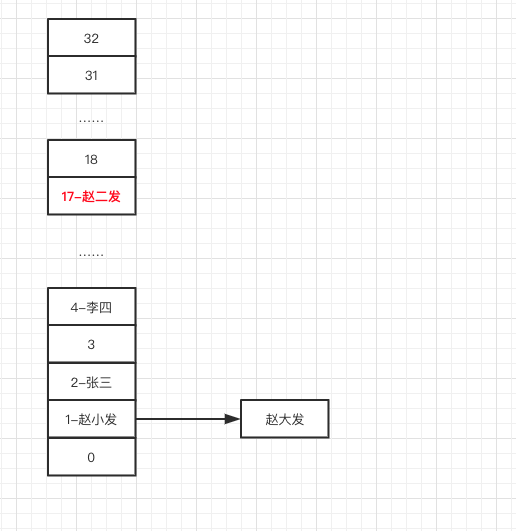
这样一个链表的 rehash 算法就完全结束了。和我们之前预想的一样，“赵小发”和“赵大发”不需要移位，“赵二发”需要移位，且新位置等于 oldIndex + oldCap 。

这篇文章到这就结束了，主要是画图一步步分析了在扩容的时候，链表是如何进行 rehash 的。